Rudders

6.1 Assumptions and Equations Used in the Design and Analysis of the Rudders

The rudder should have as small an area as possible to minimise drag. However, if the rudder is too small the sailor will loose control of the boat at low speeds. Determining an acceptable rudder size is therefore an empirical exercise. A standard rudder design shall be analysed to provide acceptable characteristics. An equivalent rudder can then be designed that will also give an acceptable level of control.

In the analysis of the rudder designs, the following assumptions and equations are used:

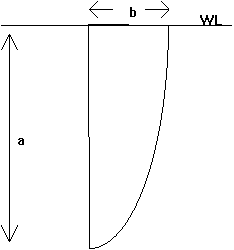1. All rudders have an elliptical spanwise chord distribution and do not twist or deflect. b = minor axis of the foil
   
   a = half the major axis of the foil
   
   s = area of the foil ( S = p a b / 4 )
   
   ARg = geometric aspect ratio ( ARg = a2 / S )
   
   
2. The effective aspect ratio of the rudder ARe is assumed to be twice the geometric aspect ratio due to the free surface boundary. Although the free surface is not a solid boundary it shall be assumed to mirror the rudder and hence
   
   ARe = 2 ´ ARg = 2 ´ a2 / S
   
   
3. A transverse foil at the tip of the rudder (used to increase longitudinal stability - see Chapter 3 ) will increase the effective aspect ratio of the rudder. From figure 6.1, The foil increases the effective aspect ratio by approximately 1.3.
   
   \ ARe = 2.6 a2 / S
   
   if the elliptical rudder has a transverse foil at its tip.
   
   
4. The transverse foil will increase the total drag of the rudder but this drag shall be ignored when rudder designs are compared.
   
   
5. The rudders have elliptical plan forms so the following relationships are true
   
   CL = k a / [ 1 + ( 2 / ARe )]
   

   where

   a = angle of attack
   k = slope of the lift of the section with angle of attack graph = dL / da
   CL = coefficient of lift
   ARe = effective aspects ratio

   CDI = CL2 / p ARe

   CD = DDP + DDI

   where

   CD = total coefficient at drag
   CDI = coefficient of induced drag
   CDP = coefficient of profile drag evaluated from graphs reprinted from "The Theory of Wing Sections" shown in figure 6.2 and 6.3

6. The maximum section thickness is 12% of the cord length. "From the data for the NACA four and five digit wing sections it appears that the maximum lift coefficients are the greatest for a thickness ration of 12 per cent." Theory of Wing Sections. As the maximum lift is a function of area, and maximum lift coefficient for the minimum area, the sections with the maximum lift coefficients must be used.

6.2 Analysis of 4 Different Rudder Designs

Design 1 - Standard Rudder

No transverse foil    -    section = NACA 0012    -    a = 0.65m    -    b = 0.2m

S = p ´ 0.65 ´ 0.2 / 4 = 0.1021m2

ARe = 2 ´ 0.652 / 0.1021 = 8.28

k = 1.3 / 12

CL = 1.3 a / [12 ´ ( 1 2 / 8.28 )] = 0.08726 a

CDI = CL2 / ( p ´ 8.28 ) = 2.927´ 10-4 x a 2

Table 6.1: Standard rudder design lift and drag characteristics.

a	CDP	CDI	CD	CL	CL/CD
0	0.0058	0	0.0058	0	0
2	0.006	1.171 x 10-3	0.00717	0.1745	24.3
4	0.0066	4.863 x 10-3	0.0113	0.3490	30.9
6	0.008	0.01054	0.0185	0.5235	28.3
8	0.0095	0.01873	0.0282	0.6981	24.8
10	0.011	0.02927	0.0403	0.8726	21.7

Design 2

Transverse foil fitted    -    section = NACA 0012    -    a = 0.65 m    -    b = 0.2 m

S = p ´ 0.65 ´ 0.2 / 4 = 0.1021

ARe = 2.6 ´ 0.652 / 0.1021 = 10.75

k = 1.3 / 12

CL = 1.3 ´ a / [12 ´ (1 + 2 /10.75 )] = 0.09134 a

CDI = CL2 / ( p ´ 10.75) = 2.470´ 10-4 x a 2

Table 6.2: Design 1 rudder lift and drag characteristics.

a	CDP	CDI	CD	CL	CL/CD
0	0.0058	0	0.0058	0	0
2	0.006	9.881´ 10-4	6.988´ 10-3	0.1827	26.1
4	0.0066	3.953´ 10-3	0.01055	0.3654	34.6
6	0.008	8.893´ 10-3	0.01689	0.5480	32.4
8	0.0095	0.01581	0.02531	0.7307	28.9
10	0.011	0.02470	0.03570	0.9134	25.6

Design 3

Transverse foil fitted    -    section = NACA 0012    -    a = 0.686 m    -    b = 0.189 m

S = p ´ 0.686 ´ 0.189 / 4 = 0.1021

ARe = 2.6 ´ 0.6862 / 0.1021 = 12

k = 1.3 / 12

CL = 1.3 a / [ 12 ´ ( 1 + 2 / 12 )] = 0.09286 a

CDI = CL2 / ( p ´ 12 ) = 2.287´ 10-4 x a 2

Table 6.3: Design 2 rudder lift and drag characteristics.

a	CDP	CDI	CD	CL	CL/CD
0	0.0058	0	0.0058	0	0
2	0.006	9.149´ 10-4	6.9149´ 10-3	0.1857	26.9
4	0.0066	3.659´ 10-3	0.01026	0.3714	36.2
6	0.008	8.234´ 10-3	0.01623	0.5571	34.3
8	0.0095	0.01464	0.02414	0.7429	30.8
10	0.011	0.02287	0.03387	0.9286	27.4

Design 4

Transverse foil fitted    -    section = NACA 64 - 012    -    a = 0.686 m    -    b = 0.189 m

S = p ´ 0.686 ´ 0.189 / 4 = 0.1021

ARe = 2.6 ´ 0.6862 / 0.1021= 12

k = 0.9 / 8

CL = 0.9 a / [ 8 ´ ( 1 + 2 / 12 )] = 0.09643 a

CDI = CL2 / p ´ 12 = 2.467´ 10-4 µ 2

Table 6.4: Design 3 rudder lift and drag characteristics.

a	CDP	CDI	CD	CL	CL/CD
0	0.005	0	0.005	0	0
2	0.005	9.866´ 10-4	5.987´ 10-3	0.1929	32.2
4	0.008	3.946´ 10-3	0.01195	0.3857	32.3
6	0.0095	8.879´ 10-3	0.01838	0.5786	31.5
8	0.012	0.01579	0.02779	0.7714	27.8
10	0.0145	0.02466	0.03916	0.9643	24.6

6.3 Rudder Design Discussion and Conclusions

It is clear from the graph in figure 6.2 comparing the designs that the effective aspect ratio has a large effect on the performance of the rudder. Of the designs presented, Design 2 is the best. Design 3 may be better when the angle of attack is below 3° (maybe 60% of the time) but NACA 64-012 section has a lower value of CL maximum; so for the same maximum lift the rudder would have to be larger. For this reason the NACA 0012 section would appear to be optimum.

A limited factor in the design of the foils is the structural consideration. Reducing b by 8% reduces the thickness of the foil by 8%. This means the second moment of area has decreased by (0.923) 22%. The centre of pressure has moved down the foil due to the increase in aspect ratio which increases the bending moment on the foil. The aspect ratio is therefore limited by structural considerations. It shall be assumed that an effective aspect ratio of 12 is achievable without an excessively heavy structure.

The profile of the rudder should be modified to a crescent form as seen in "Letters to Nature". This type of plan form is shown to have 4.3% less induced drag for 1.5% less lift than the standard rudder shape (with a straight trailing edge) at a = 4%.

The theoretical calculated values of lift and drag are based on a plan form with a straight ¼ cord line (wing 1) and therefore must be modified to take account of plan form

Diagram of foil profiles: (not available on this site at present)

Table 6.5: Correction factors for profile shape on rudder lift and drag coefficients.

Wing	CDI	CL	fI	fL
1	0.00531	0.34157	1	1
2	0.00510	0.34236	0.96	1.002
3	0.00475	0.33714	0.89	0.987

The above data helps to support the analysis of the effect of angle of sweep in Chapter 5. Wing 3 has a larger effective angle of sweep than Wing 1 and has less induced drag for less lift.

Taking into account the profile of rudders, the lift and drag can be calculated as follows.

L = ½ ´ r´ V2 ´ S ´ fL ´ CL

where

r = density of water = 1025 kg / m3
V = velocity taken as 5 knots = 2.87 m/s
S = area of foil = 0.1021m2
FL = correction factor
CL = coefficient of lift

D = ½ r V2 S(CDP + fI CDI)

where

CDP = coefficient of profile drag taken from graph for section
CDI = coefficient of induced drag
fI = correction factor

The final design can be compared to the original rudder and actual values of lift and drag compared. The drag of the transverse foil, which offsets the drag curve, can be included. (Note a for transverse foil assumed to be 0° .)

Ideally the boat would be equipped with 2 rudders, one without a foil for light winds and one with a foil for stronger winds where longitudinal stability is a problem.

Standard Rudder

(no transverse foil)     -     ARe = 8.28     -     S = 0.1021 m2     -     section = NACA 0012

Table 6.6: Actual values of lift and drag for a Standard rudder at 5 knots.

a	CDP	fI CDI	fL CL	D Newtons	L Newtons
0	0.0058	0	0	2.5	0
2	0.006	1.124´ 10-3	0.1748	3.1	75
4	0.0066	4.496´ 10-3	0.3497	4.8	151
6	0.008	0.01012	0.5245	7.8	226
8	0.0095	0.01798	0.6995	11.8	302
10	0.011	0.02810	0.8743	16.9	377

 Design 2

(with transverse foil at zero angle of attack)     -     CDI for transverse foil = 0     -     CDP = 0.004 for NACA 65.012
S = 0.04 = area of foil     -     D = additional transverse foil drag

D = ½ r V2 S(CDI + CDP)

D = 1025 2.872 ´ 0.04 ´ 0.004 / 2 = 0.675 Newtons

Rudder Details

AR = 12     -     S = 0.1021     -     Section = NACA 0012

D = ½ R V2 S ( CDP + fI CDI ) + 0.675

Table 6.7: Actual values of lift and drag for a design 2 rudder with foils at 5 knots.

a	CDP	fI CDI	fL CL	D Newtons	L Newtons
0	0.0058	0	0	3.2	0
2	0.006	8.143´ 10-4	0.1833	3.6	79
4	0.0066	3.257´ 10-3	0.3666	4.9	158
6	0.008	7.328´ 10-3	0.5499	7.3	237
8	0.0095	0.01303	0.7332	11.4	316
10	0.011	0.02035	0.9165	14.2	395

Design 2

(with no foil)     -     Section = NACA 0012     -     S = 0.1021 m2     -     AR = 0.6862/ 0.1021 = 9.22

CL = 1.3 a / [ 12 ´ ( 1 + 2 / 9.22 )] = 0.08902 a

CDI = CL2 / ( p ´ 9.22 ) = 2.736´ 10-4 a 2

Table 6.8: Actual values of lift and drag for a design 2 rudder without foils at 5 knots.

a	CDP	fI CDI	fL CL	D Newtons	L Newtons
0	0.0058	0	0	2.5	0
2	0.006	9.740´ 10-4	0.1757	3	76
4	0.0066	3.896´ 10-3	0.3515	4.5	151
6	0.008	8.766´ 10-3	0.5272	7.2	227
8	0.0095	0.01558	0.7029	10.8	303
10	0.011	0.02435	0.8786	15.2	379

 

A graph comparing the calculated data above is shown in figure 6.5.

The tip of the foil will have to be slightly modified to accommodate the transverse foil. The section may also have to be increased in thickness by using a NACA 0015 section at the very tip. This will make the tip stronger and the foil less likely to break off.